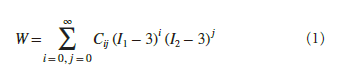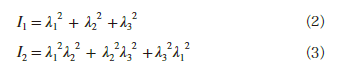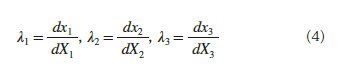電力機器の更なる信頼性向上と開発設計の
効率化に向けた気密構造のゴム解析技術

北村 拓真　Takuma Kitamura 森 佑介　Yusuke Mori 滝澤 明広　Akihiro Takizawa

電力機器には絶縁油や絶縁ガスが封入されているものが多い。これらが内部から漏れないように，または，外部から水などが侵入することを防ぐために，気密構造が必要であり，その気密を確保するための材料として，ゴム材料が広く使用されている。ゴム材料を潰したときの反発力を利用して，機器の気密を確保しているが，ゴム材料の特性上，力の大きさと変形量が比例すると仮定した単純な材料力学では，詳細を把握することができない。そこで本稿では，製品の品質向上や試作回数の削減，開発設計の効率化に繋がるゴム材料の解析技術について，実測と解析の結果の比較検証例や解析技術の製品への活用方法を交えて紹介する。

1はじめに

気密構造は，多くの製品で気密を確保するために必要であり，気密構造部分には様々な材料が用いられている。特に電力機器には，電気を絶縁するために絶縁油や絶縁ガスが封入されているものが多く，内部からの漏れ，または，外部から水などの侵入を防ぐために，気密構造の検討が重要となっている。気密構造部では，ゴム材料の反発力を利用し，気密を保つことが多い。

満足な気密性能を得るためには，ゴム材料を適切に潰し，十分な接触面圧を確保する必要がある。しかし，ゴム材料はその特性上，力の大きさと変形量が比例すると仮定した単純な材料力学では，気密性能の評価で重要となるつぶし代や面圧分布などを把握することができず，構造解析を行うには一般的に難易度が高い。そのため，気密構造を有する機器の開発においては，長年の製品実績をベースとした設計と繰り返しの試作評価により，製品品質を担保してきた。

今回，製品の品質向上や試作回数の削減，手戻り防止による開発設計の効率化を目的としてゴム材料の特性を考慮した解析技術に取り組んだ。

本稿では，ゴム材料を使用した気密構造の解析技術として，ゴム解析技術の特徴と製品設計への活用例について紹介する。

2ゴム材料の特徴

ゴム材料は，力を加えると大きく変形するが，力を除くとほぼ元の形に戻るという特徴から，その際の反発力を利用して，気密を確保するための材料として広く使われている。

気密構造の開発設計をする際に重要となる機械的特性面での特徴を4つ紹介する。

（1）応力-ひずみ特性において，強い非線形性を有する

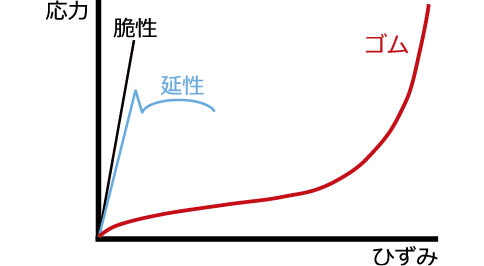
1つ目は，応力-ひずみ特性において，強い非線形性を有することが挙げられる。脆性材料と延性材料，ゴム材料の応力-ひずみ特性を図１に示す。脆性材料は，ひずみの増加に伴って応力が上昇し，ほとんど塑性変形せずに破壊する。延性材料は，降伏点までは線形だが，それ以降は非線形性を示し，やがて破断する。ゴム材料は，最初は少ない力で大きく伸びるが，あるところから伸ばすために必要な力が大きくなる。また，他の材料と比較しても，破断するまでに大きく変形する。このように，ゴム材料は強い非線形性を示すため，気密構造の検討を手計算で求めるのが難しい材料となっている。

（2）非圧縮性であり，変形前後で体積が変化しない

2つ目は，非圧縮性であり，変形前後で体積が変化しない特徴を有している。物体に対して荷重を加えたとき，一般的な金属材料やプラスチックは変形に伴って体積も変化していくが，ゴム材料は荷重によって形が変わっても，変形の前後で体積がほぼ一定に保たれる非圧縮性という特性を有する。

（3）変形回数によって，変形挙動が変化する

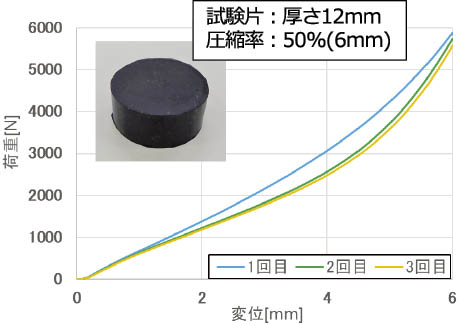
3つ目は，変形回数によって，変形挙動が変化する特徴がある。円柱状のゴム材料を用いてゴムの圧縮試験時の高さ方向の変位と荷重の関係性を確認した結果を図２に示す。図２より，圧縮1回目と2，3回目で変形挙動が異なっていることがわかる。このように，変形挙動が変わることで，ゴム材料の物性値も変化するため，ゴム材料を解析するときには，何回目のデータを用いるべきなのか，製品の用途に合わせた運用が必要となる。

（4）永久ひずみが生じる可能性がある

4つ目は，永久ひずみが生じる可能性がある点にも注意が必要である。ゴム材料は荷重状態を長時間保つと，除荷しても完全には元の厚さに戻らないことがある。この元の厚さに戻らなかった差分を永久ひずみという。永久ひずみが残ってしまうと，元の形のときと比べてゴム材料の反発力が低下するため，面圧が確保できなくなり，気密が保てなくなる可能性がある。

これらの特徴を踏まえ，ゴム材料を用いた気密構造を解析するために，次章に示すような方法でモデル化がされている。

3ゴム材料のモデル化方法

ゴム材料は，一般的な弾性材料のようにヤング率^注1)とポアソン比^注2)のみで材料物性をモデル化することができない。そこでゴム材料を超弾性体として扱うことで，ひずみエネルギー関数を用いてモデル化される。ひずみエネルギー関数とは，物質を変形させたときに，その物質内に蓄えられる単位体積当たりのエネルギーのことをいう⁽¹⁾。このひずみエネルギー関数には，様々な種類の表現式が提唱されており，代表的なひずみエネルギー関数の定義式として，Neo-HookeanやMooney-Rivlin，Ogden⁽²⁾などのモデル式がある⁽³⁾⁽⁴⁾。その中で，精度が高く比較的単純な形で扱いやすいことから，今回使用した一般化Mooney-Rivlinの式を式（1）に示す。

ここで，Iは不変量，λは伸長比であり，それぞれ式（2）～（4）で表される。不変量は，主応力や相当応力など，座標系によらず変化しない量のことで，伸長比は，変形前後の長さの比率を表す。

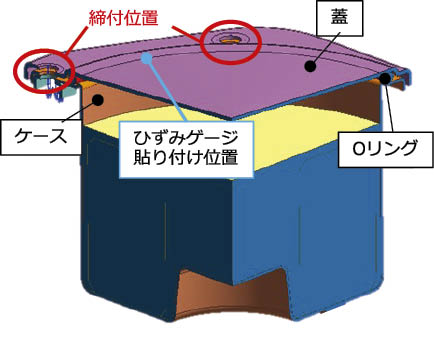
4実測と解析の結果比較

実測と解析の結果を比較するために用いたモデルを図３に示す。モデルは蓋とケースの間にOリングを接触させ，ボルトで締め付けることで気密を確保するものである。なお，Oリングにはクロロプレンゴム（以下，CR）を用いた。解析では，供試器の対称性を考慮して計算時間短縮のために1/4モデルとし，締付位置の上面から鉛直下向きの荷重を設定して，解析を行った。

実測では，面圧分布と，ゴムの反発力による構造物のひずみを測定項目とした。面圧分布は，感圧紙をケースの上に乗せ，その上にOリングを配置する方法で測定した。ひずみは，締付部中間位置の平坦な部分にひずみゲージを貼り付け，ゴムの反発力による蓋の変形を測定した。

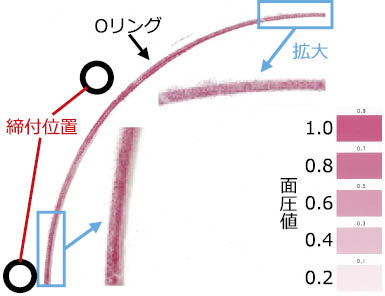
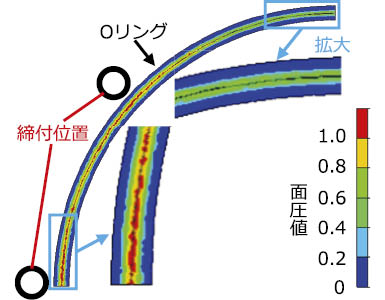
面圧分布の実測結果を図４に，解析結果を図５に示す。面圧値は，実測で発色される最も濃い赤色を1として基準化表示している。

図４および図５より，実測，解析ともにOリングの全周にわたって面圧が確保されていることが確認できる。締付部付近と締付部から離れた箇所の拡大図を見ると，実測および解析とも締付部付近の面圧が強くなっている。また，合わせて実施したひずみ測定においては，実測と解析の差が10％以下であったことを確認している。

以上のように，Oリングの面圧分布や反発力によって生じる構造物のひずみ量が，実測と解析で一致することを確認した。

5ゴム解析技術の活用例

ゴム解析技術の活用例として，開発設計時に締付位置やゴム材料を変更したときのつぶし代および面圧の可視化事例を示す。例として，長方形の蓋とケースの間に，CRを使用した角パッキンを挟んだモデルを作成し，解析を行った。以降の解析結果では，蓋やケースは非表示にして角パッキンのみを表示しており，図中黒枠の丸は，締付位置を表すこととする。

5.1　気密構造部の締付位置の検討

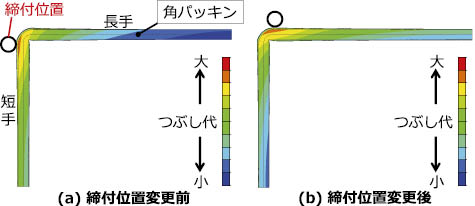
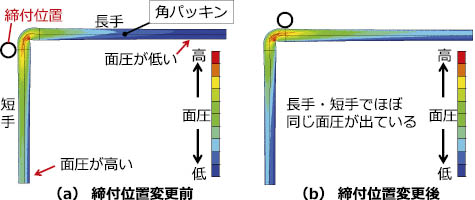
締付位置変更前後のつぶし代および面圧分布の解析結果を図６，図７に示す。変更前の解析モデル（a）では，モデルの短手側をボルトで締め付けているが，長手側のパッキンのつぶし代は小さく，面圧も低い。そこで，解析モデル（b）のように締付位置を長手側に変更することにより，長手部分のつぶし代は大きく，面圧も高くなり，均一な接触面圧が確保できていることがわかる。

5.2　気密構造部のゴム材料硬度の影響

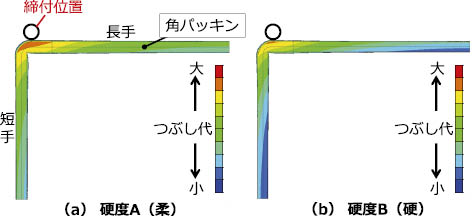
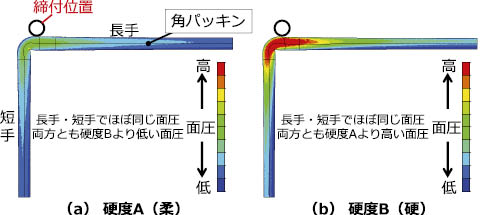
前節の解析モデルから，ゴム材料の硬度を下げた場合（以下，硬度A）と上げた場合（以下，硬度B）のつぶし代および面圧分布をそれぞれ図８，図９に示す。

ゴム材料の硬度を変更した解析結果より，硬度Aは，同じ締付力であってもつぶし代は大きくなるが，面圧は低くなる。一方で，硬度Bでは，つぶし代は小さく，また，局所的に面圧は高くなるといった挙動が明確に可視化できている。

6おわりに

本稿では，電力機器に用いられているOリング，角パッキンを対象としたゴム解析技術を紹介した。

今回紹介したゴム解析技術を用いることで，ゴム材料の挙動を可視化できるため，気密性能を評価する上で重要なゴム材料のつぶし代や面圧分布などを詳細に把握できるようになり，より適切な気密構造の設計が可能になる。

今後は，このゴム解析技術の適用拡大により，製品の品質向上や試験回数削減，手戻り防止による開発設計の効率化に繋げていきたい。

■参考文献

（1）河村幸伸，浦山健治，粷谷信三，深掘美英：「エラストマーのひずみエネルギー密度関数の解析」，日本ゴム協会誌，第73巻，第1号，（2000）

（2）R.W. Ogden：「Large deformation isotropic elasticity–on the correlation of theory and experiment for incompressible rubberlike solids」，PROCEEDINGS OF THE ROYAL SOCIETY A，Vol.326，pp.565-584，（1972）

（3）石川覚志：「〈解析塾秘伝〉ゴムの有限要素法の学び方！ ―超弾性体の基礎理論と実践―」，日刊工業新聞社，（2015）

（4）萩本光広：「ゴムのFEM解析―初心者から中級者のためのはじめの一歩基本のすすめ―」，銀河書籍，（2018）

（5）R.S. Rivlin，D.W. Saunders：「Large elastic deformations of isotropic materialsⅦ． Experiments on the deformation of rubber」，PHILOSOPHICAL TRANSACTIONS OF THE ROYAL SOCIETY A，Vol.243，pp.251-288，（1951）

■語句説明

注1) ヤング率：縦弾性係数とも呼ばれる。材料の変形のしにくさを表す物性値。

注2) ポアソン比：荷重をかけた方向のひずみ量に対して，それと垂直方向のひずみ量の比率を表したもの。